
黄霖1,2,黎源1,2,汪星辰1,2,赵运磊1,2
1. 复旦大学计算机科学技术学院,上海 201203
2. 上海市数据科学重点实验室,上海 201203
(引用标注:黄霖,黎源,汪星辰,等.数据自治开放的加密技术挑战[J].大数据,2018,4(2),50-62.)
摘要:数据自治开放以数据盒为基本数据单元向数据使用者开放,因此数据资源稀缺性丧失和隐私泄露等问题的防范主要针对数据盒。一个数据盒可能包含照片、视频、文本和结构化数据等,传统的数据加密技术无法有效应用。系统分析了数据盒对数据加密的需求和传统数据加密技术面临的挑战,探讨了面向数据自治开放的加密新型技术的展望。
关键词:数据自治开放;对称可搜索加密;属性保留加密;属性揭示加密;同态加密;不经意随机存取
Abstract: Data box is the basic data unit opened to the data users in self-governing openness of data,so the prevention for the degradation of data scarcity and the disclosure of privacy is mainly aimed at the data box.A data box may contain photos,videos,text and structured data,etc.The traditional data encryption technology cannot be effectively applied.The requirement of data encryption for data box and the challenges of traditional data encryption technologies were analyzed,and the prospect of new encryption technologies for self-governing openness of data was discussed.
Key words: self-governing openness of data ; searchable symmetric encryption ; property-preserving encryption ; property-revealing encryption ; homomorphic encryption ; oblivious random access memory
1 引言
随着大数据时代的来临,各行各业产生并收集的数据量日益增长。愈来愈多的政府、企业以及个人开始重视数据的严格定义、规范产生、安全存储、约束读取以及有效分析。因此,对数据进行自治开放、开通获取和利用的渠道已成为当代数据科学和业界的重要共识和发展方向。
“数据盒”模型是一个面向数据开放共享的数据模型,它由为数据使用者提供开放数据的基本组成单元——数据盒、封装在数据盒中的数据防泄露和数据权益保护机制、数据盒的计量与定价组成。数据拥有者将数据灌装入数据盒中,封装的数据只能通过数据盒中的自主程序单元接口进行受控的访问,使得数据使用者既方便使用开放数据,即外部可见、可理解、可编程,又能防止数据拥有者权益受到侵犯,即内部可控、可跟踪、可撤销。
目前,数据的开放共享极易导致数据资源稀缺性丧失,部分数据也存在隐私泄露的风险。在数据盒中数据的版权和隐私保护若采用传统的私钥加密和公钥加密(如高级加密标准(AES)、RSA等),数据的操作需要用户将密文全部下载到客户端,解密后执行。这种应用架构明显具有吞吐量低、带宽需求大、可用性差的缺点,无法在大数据场景下得到有效应用。
面向大数据时代自治开放的需求,发展支持密文域处理的新型数据访问安全技术是当前密码领域的研究热点。2011年Popa R A等人[1]发表了第一个实用的数据访问安全技术CryptDB,大量的数据访问安全技术被学术机构和商业公司开发出来并应用,例如:Ciphercloud、Google’s Encrypted BigQuery、Skyhigh等。
在支持密文域处理的数据访问安全技术中,全同态加密(fully-homomorphic encryption,FHE)[2]和不经意随机存取(oblivious random access memory,ORAM)[3]作为具有计算普适性的一类,其高带宽需求、高计算量、存储复杂度和多轮次数据通信大大降低了实际应用的可能性。因此,可搜索对称加密(searchable symmetric encryption,SSE)、属性保留加密(property-preserving encryption, PPE)、属性揭示加密(propertyrevealing encryption,PRE)、同态加密(homomorphic encryption,HE),甚至SQL语句重写模型(SQL-aware rewriting model,SRM)是目前较为实用的支持密文域处理的数据访问安全技术,它们的发展也对数据自治开放中的隐私保护起到了很大的作用。
上述的底层算法、技术和整个数据访问安全技术,其发展都是不断寻求些许的单方面突破以及效率、安全性、易用性和适用性等之间的平衡。目前也并没有一个系统或底层算法有绝对的优势,因此,本文旨在基于数据自治开放的大背景,梳理现有支持密文域处理加密算法和架构技术的优劣,一方面引起国内学术界和商业界对数据安全和支持密文域处理的数据访问安全技术的重视,另一方面为将来的学术研究理清脉络,展现重点与难点。
本文的贡献有以下几点:
●基于自治开放的需求,分析数据盒访问面临的数据安全挑战;
●研究数据访问安全技术底层的密文查询技术,涵盖可搜索对称加密、属性保留加密、属性揭示加密、同态加密以及较不实用的全同态加密和ORAM,分析并归纳其用途、信息泄露、功能完备性以及安全性和效率的权衡;
●针对确定性加密、可搜索对称加密、属性保留加密和属性揭示加密,研究现有的不同攻击,分析其敌手能力要求、攻击目标、先决条件和效率等;
●归纳查询转换技术,基于复杂查询可由基本查询转换而来的思想,分解难以实现的复杂查询,降低底层技术需求,分析数据访问系统基础功能的转换盲区;
●分析现有支持密文域处理的数据访问安全技术,归纳其支持功能、安全性、效率和附加功能等方面的优劣。
2 数据盒访问的数据安全挑战
2.1 威胁模型和安全挑战
概括地说,数据访问安全技术的设计主要是为了应对两种安全威胁[1], 即来自外部的侵入系统窃取数据的黑客和网络信道的数据观测者、来自内部的监守自盗的数据库管理人员。针对两种安全威胁,数据访问安全技术多用于私有云场景。这是典型的双方场景,数据提供者和数据查询者由同一人扮演,再与服务器进行交互。也有一种应用场景是数据提供者和数据查询者由不同人扮演,与服务器进行交互。绝大多数的数据访问安全技术没有考虑实施数据规则制定与实施监管的问题。CryptDB采用了洋葱分层加密的思想提高安全性,并进行有效的效率保障。同时,其针 对TPC-C规范中事务处理的吞吐量下降较少,因此获得广泛认可和借鉴。
对于数据盒,数据访问安全技术的挑战按照攻击者来源可分为以下两种。
(1)内部攻击者的挑战
在数据盒正常使用的情况下,需要在明文上进行查询,这时好奇的管理员/第三方平台维护人员可能窥探到数据,这明显会侵害数据拥有者在数据自治情况下的利益。在这种威胁下,数据访问安全技术可以防止好奇的管理员访问数据盒中的真正数据。解决方案是:在灌装数据盒前,通过特定的非传统私钥、公钥加密方法对数据盒中的数据进行加密,从而在交互模块中直接对密文进行查询,将查询结果返回给用户。
(2)外部攻击者的挑战
在数据盒被盗取或控制的情况下,来自外部的黑客和网络信道的数据爬取者可能侵入系统窃取数据,同时控制数据源管理模块、交互模块等多个模块。这时虽然第一种挑战的解决方案有助于保障被盗取的数据呈现密文形态,不泄露明文,但其难以应对暴力破解或者特定的攻击方式。解决方案是可以采用不同的密钥加密不同的数据字段。在这种情况下,只有在攻击者侵入并获取数据拥有者的所有加密私钥的情况下,才有可能导致此用户的数据泄露。此外,在发现有人不正当使用数据盒时,还可以启动数据盒自毁机制。
依据挑战的威胁程度,可以将挑战分为以下3种。
●快照挑战:敌手仅能获取某一时刻的数据信息,无法获取动态的数据更新信息。这是最弱的挑战威胁,绝大多数数据访问底层加密技术均可保障这种情况下的隐私安全。
●监测挑战:敌手仅能持续获取数据,相对于快照挑战,能够额外获得动态更新的数据信息。
●访问挑战:敌手不仅能够获取时刻更新的数据信息,同时还可以伪造数据进行测试、推理与攻破。这是攻击者能力极强的一种挑战,当前应对这种挑战的数据访问底层加密技术可能效率较差。
2.2 数据信息泄露模型
即使采用数据访问底层加密技术应对以上挑战,依然会有不同的算法泄露些许不同的数据信息。本节介绍的数据个数、数据基本结构、查询、查询回复记录和访问控制与模式等消息易被数据访问安全技术泄露。即使其中有诸多内容是以密文形式出现的,其加密算法本身造成的信息泄露也扩大了明文有效恢复的几率与途径。
基于普遍使用的底层加密算法,现归纳5种宏观的泄露类型,以危害程度递增、安全性递减方式排列。
●数据结构:此处的数据结构是广义的,包含诸如字符串长度、集合内元素数量、树型数据结构等内容。它们是由数据访问存储基本模式泄露的,除非执行内容填充和结构置换等操作,否则难以进行隐藏。
●数据标识符:一些底层加密算法将数据额外存储,以其指针作为加密基元,因此数据标识符(或指针)的泄露相较于等值信息泄露危害较小。
●多重辅助判断信息:包括数据标识符信息和其余辅助信息。例如多个数据位于同一已知范围、且由同一数据插入操作导入等信息。
●等值信息:数据相等的信息。
●顺序信息:数据之间大小关系的信息。
绝大多数的信息泄露发生在数据查询操作时,诸如数据结构、等值信息和顺序信息可能在数据初始化操作时就已经泄露(例如,使用确定性加密[4]或保序加密[5,6]时可能发生此情况),而数据更新操作可能会有较少的信息再次泄露。
3 安全数据访问基本查询技术
在数据自治开放情况下,为了保证敏感数据可用性,同时保证敏感数据的保密性,防止敏感数据被窃取,可以使用数据访问安全技术进行加密。数据底层加密技术主要有3类加密算法:以源数据进行加密的传统加密(不是诸如AES、RSA之类的传统加密);以源数据指针进行加密的自定义加密;主要以ORAM为算法基础的Oblivious加密。
3.1 属性保留和属性揭示加密
绝大多数的属性保留加密[7]和属性揭示加密都是传统加密,它们的构造是为了方便密文对对应的操作产生正确的反应,将密文返回并解密,得到正确的明文结果。此处的“属性”主要是指“等值”属性和“顺序”属性,因此绝大多数确定性加密[4]、保序加密[5-11](或顺序保留加密)和揭序加密[12-14](或顺序揭示加密(order-revealingencryption,ORE))都是传统加密算法。在数据的自治开放中,它们既可以使权限拥有者能够进行一些数据查询(如找到最大值)操作,又能对数据进行保密操作,使拥有查询权限者无法得知数据访问系统中存储信息的具体值。
确定性加密是“将相同的明文加密成相同的密文”的加密算法,理想的泄露情况是其他的属性信息完全隐藏。此外,绝大多数保序加密和揭序加密都是确定性加密。
保序加密具有通过密文比较得出明文大小关系的特质。2004年Agrawal R等人[8]首先给出了关于保序加密方案的概念、定义和一种构造数值型保序加密方法。此后5年,关于保序加密的相关研究一直未能有较大突破。直到2009年,Boldyreva A等人[5]才对该问题有了较为系统的研究。首先,作者提出了关于保序加密的严格安全定义(IND-OCPA,即关于保序加密理想的安全性,也即前文所述的理想顺序泄露状态)。为了使方案的构造成为可能,作者对安全模型的安全性进行了一定程度的放松。随后,作者试图通过超几何分布这一工具得到一个映射,使得该映射在多项式级别的敌手看来与理想对象是不可区分的。这一方案便是前文描述的基于随机保序函数产生泄露的方案。在2011年,Boldyreva A等人[6]对保序加密方案的安全性进行了更为深入的分析。他们提出了窗口单向性(window onewayness)和距离窗口单向性(distance window one-wayness)的概念,针对这些安全定义给出了保序加密对应于它们的上界和下界。同时,作者指出其在2009年提出的保序加密方案[5]会泄露明文一半的比特位。
为了构造足够安全的保序加密,Popa R A等人[11]于2013年另辟蹊径,打破了传统保序加密算法非交互的框架,转而采用交互的框架,使构造的保序加密方案满足理想的安全性。基于Popa R A的交互框架, Kerschbaum F和Schropfer A[10]受到随机二叉搜索树的平均高度相关研究的启发,将方案的平均通信复杂度由O(nlogn)缩减到了O(n)。随后,Kerschbaum F[9]为了设计出具有更强安全性的保序加密方案,构造了具有频率隐藏性质的保序加密方案。不同于之前的所有确定性的保序加密方案,该方案使敌手无法区分两个相同明文的密文。该算法采用的方法是客户端在与服务器交互的过程中对于等值的数据随机回复大于或小于。
2015年Boneh D等人[12]受到了密码学混淆器的启发,提出了一种新的能够提供比较密文相应明文大小功能的加密方案,即揭序加密。作为保序加密的泛化,揭序加密中密文对应明文的顺序无法直接通过比较密文数值的大小来确定,而是借助了公开的比较函数。出于实用性考虑,Chenette N等人[14]在效率和安全性之间做出了一定的权衡,构造了第一个实用的只泄露有限明文信息却高效的揭序加密方案。该文章首次基于泄露函数制定安全定义,证明了构造的方案只泄露了任意两个密文的第一个不相同的最高比特位。同时,该方案的构造只使用了伪随机函数这一密码学工具,方案具有极高的效率。最近,Cash D等人[13]提出了一个相比Chenette N等人提出的方法算法安全性更高的揭序加密方案,但是由于需要使用一种新型的、基于双线性图的属性保留函数,计算效率较差。
3.2 自定义加密
绝大多数可搜索加密属于自定义加密,也有一些其他加密方法属于此类。在自治开放中,如果数据使用者需要用到搜索操作,但不知道具体数据,则可使用自定义加密。自定义加密的构造主要依据反相指数查找和树型遍历两种方案。
关于反向指数查找方案,不少工作都涉及反向查找单一数据表并映射关键字到标识符列表的技术。诸多的工作为其提供了额外的特性,Bost R[15]提出了依赖陷门置换的、较为实用的公钥可搜索加密,实现了前向安全与后向安全。目前前向安全的揭序加密算法也已设计出来,属于传统加密方案。
关于树型遍历方案,Kamara S等人[16]展示了一种可平行方法以支持等值查询,通过足够多的平行处理,该算法的查询复杂度可在摊销后达到常数级。Stefanov E等人[17]也利用类似的方法,首次正式提出并设计了前向安全的可搜索加密算法。此外,树型遍历方案也满足范围查询。非关系型数据访问安全技术Arx[18]中的Arxpange算法通过建立明文简历存储与二叉树的索引,实现不泄露所有数据的顺序关系的范围查询。利用Yao A C[19]的乱码电路,可以实现服务器在遍历索引时无法获得比较的数据的值与比较结果。值得额外一提的是,Roche D S等人[20]提出并实现了一种基于缓冲区二叉平衡树的部分保序加密,它是一种针对多数据插入、少范围查询应用场景的属性保密加密。不同于Popa R A等人和Kerschbaum F的树型保序加密算法,该算法将数据提供者和服务器的交互排序环节置于数据查询阶段。也正因如此,该算法实现了至今最高的安全性——基于频率分析的偏序选择明文攻击的不可区分性(IND-FA-POCPA)。
3.3 Oblivious加密
ORAM由于其极强的安全性,在近20年里一直作为重要的研究课题,并且在性能上有了稳步的提升,其中诸多最近算法的实现是基于PathORAM算法[21]的,性能方面的优化也有Garg S等人[22]的TWORAM算法可参考,该算法致力于缩减搜索操作的回合。鉴于其目前仍具有高带宽、多数据轮次和高客户端存储等需求,以ORAM为基本算法的可操作性数据加密仍然不具有广泛的适用性,此外由于其不是数据自治开放情况下数据访问安全技术发展的重点,不再赘述其相关工作。
3.4 同态加密
同态加密是一种具备特殊性质的加密。在数据自治开放中,同态加密可以使数据使用者对密文进行特定运算,其结果为对应明文执行相应运算后的密文,即对密文的运算等价于对明文执行相同的运算,而数据使用者并不能知道数据的具体值。同态的性质使其在云计算、外包计算、安全多方计算、数据访问安全技术等多个领域有着极大的应用前景。
对于乘法同态加密,较为代表性的例子当属经典的RSA加密[23]和ElGamal加密[24],而Paillier加密[25]和GM加密方案[26]则具备加法同态性质。为了使同态加密能够支持更广泛的运算操作,2005年由Boneh D等人[27]利用双线性映射构造了支持对密文进行一次同态乘法运算和任意次同态加法运算的同态加密方案。
2009年,Gentry C[2]首次提出了全同态加密的概念,它支持对密文进行任意次数的同态加法和同态乘法运算。同时,Gentry C基于理想格构造出了第一个全同态加密方案。然而,由于Gentry C方案的效率极低,使其仅具有理论意义。
Van D M等人[28]在2010年首次给出了基于整数的全同态加密方案。基于整数的思路,从缩减密钥规模[29]、缩减密文规模、提升计算效率[30]等方面构造优化的全同态加密方案,其采用的技术路线主要是压缩公钥、密文批处理、统一模数等。与基于理想格的全同态加密相比,基于整数的全同态加密具有更为简单的代数结构,使得方案更易于理解和分析。
LWE(learning with error)问题为许多密码学方向指出了新的突破思路,Brakerski Z等人[31]也尝试基于LWE问题构造全同态加密方案。随后,Brakerski Z等人[32]基于LWE问题给出了一个摆脱Gentry C框架的新的构造思路,其主要基于LWE问题构造部分同态加密方案,然后利用模数转换技术达成替换压缩解密电路技术的目的。之后,Gentry C等人[33]针对降低同态计算的计算复杂度给出了解决方法,技术路线主要是解除对电路深度的依赖,从而使计算复杂度与电路深度无关。
结合数据自治开放模型,可以根据数据即将使用或惯用的查询操作,结合各方面要求,预先定义(对于数据盒则在灌装时定义)或自适应地[1]对相关数据采取最合适的加密方式,如范围查询使用保序加密和揭序加密;在需要用到搜索操作而不能知道具体数据时,使用可搜索加密;在需要对数据进行运算时,采用同态加密。这些不同的加密方式均可以在保证数据自治开放的同时,防止数据盒中数据泄露,保护数据权益。
4 安全数据访问查询转换技术
在数据自治开放中防止敏感数据泄露的同时,数据查询的有效性也是一个重要的课题。安全数据访问查询转换技术可以有效地将复杂的查询转换成其他查询的组合,这样可以有效扩充数据访问安全技术的功能集,也可以有效减少数据访问安全技术的程序大小。弊端是可能额外增加计算复杂度和临时存储复杂度。现定义以下基本查询和操作的表述符号,以便后文安全数据访问查询转换技术的描述,见表1。
表1 基本查询及操作的表述符号
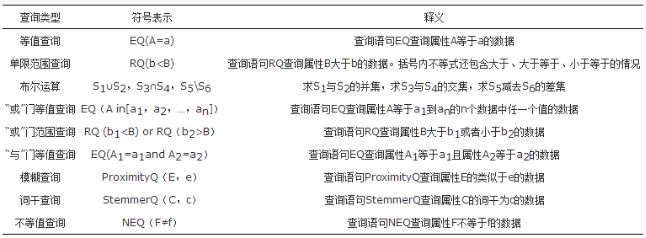
现罗列可执行的查询转换如下。
●双限范围查询转换为单限范围查询和布尔运算:
RQ(b1<B≤b2)→RQ(b1<B)∩RQ (B≤b2)
●等值查询转换为范围查询:
EQ(A=a)→RQ(a≤A≤a)→RQ (a≤A)∩RQ(A≤a)
● “或”门等值、范围查询转换为等值、范围查询和布尔运算:
EQ(A in[a1,a2,…,an])→EQ (A≤a1)∪EQ(A≤a2)∪…∪EQ(A≤an)
RQ(b1<B)or RQ(b2>B)→RQ (b1<B)∪RQ(B<b2)
● “与”门等值查询转换为等值查询和布尔运算:
EQ(A1=a1and A2=a2)→EQ(A1=a1)∩EQ(A2=a2)
●模糊查询转换为等值查询:模糊查询用来查询与关键字相近的数据,一种方法是将字符串数据拆分,每两个相邻字符组合构成新的列,根据等值查询数据匹配计算相似度,另一种较为简便的方法是利用局部敏感散列,相关的距离计算或相似度计算也可以专门优化。
●词干查询转换为等值查询:针对查询相同词干的字符串,若想转换为等值查询,需要在数据初始化和导入阶段添加额外的数据列,并存入其对应的词干密文数据。然后改写查询:
StemmerQ(C,c)→EQ(D=c)
●小范围查询转换为等值查询和布尔运算(可枚举):
RQ(b1<B≤b1+2)→EQ(B=b1+1)∪EQ(B=b1+2)
●大范围查询转换为等值查询和布尔运算(不可枚举):此情况需要构造特定数据存储结构,如利用[0,256)的数据构造一个二叉树,每个数据作为完美平衡二叉树的叶子节点,且生成新的层范围列,记录每层所属区间。例如:33这个数据需要生成层范围列,并记录B1:[0,256)、B2:[0,128)、B3:[0,64)、B4:[32,64)、B5:[32,48)、B6:[32,40)、B7:[32,36)、B8:[32,34)、B9:[33,34)。若查询大于33且小于等于58的数据可进行如下转换:
RQ(33<B≤58)→RQ(34≤B<59)→EQ(B8=[34,36))∪EQ(B7=[36, 40))∪EQ(B6=[40,48))∪EQ(B6=[48, 56))∪EQ(B8=[56,58))∪EQ(B9=[58, 59))
●不等值查询转换为范围查询和布尔运算:
NEQ(F≠f)→RQ(fmin≤F<f)∪RQ (f<F<fmax)
●连接语句转换为不同表不同列等值查询:这一种转换需要在数据访问安全技术不同表不同列在同一权限下确定性加密密钥一致(即相同明文在不同表不同列的密文一致)的情况下,才可使连接语句转换为两层循环的不同表不同列等值查询。
●字符串的子串以及通配符查询:这两者均需要产生并利用极多的附加列,在初始化和数据导入阶段,依据子串和通配符长度查询需求,进行子串列的枚举式构造,以便拆分改写子串查询语句和通配符查询语句。由于增加了多次遍历,因此大大增加了计算复杂度。
除了上述的查询转换技术,仍有许多常用的数据访问操作未能以数据访问安全技术实现。例如基于自定义加密算法和Oblivious加密算法的笛卡尔积运算(即连接查询)、矩阵的乘法、字符串的大小比较等。
在数据盒中,结合不同查询,应用不同的合适的安全数据访问查询转换技术,可以提高数据查询的有效性,便捷地保障数据盒在加密保护机制下的功能性。
5 数据访问安全技术
近年来,数据的自治开放已成为当下数据价值开拓的重要课题,数据访问安全技术也成为业界倍加关注的方向。其中大多解决方案保证了数据访问系统的绝大多数基本功能,同时保障了数据的机密性,即以些许信息泄露为代价,对加密的数据执行有效操作。
在数据加密方面,麻省理工学院(MIT)的CryptDB项目首先打开了大门,证实了密文操作数据访问系统的可行性和实用性,也展示了未来发展的方向与瓶颈,随后Google公司的Big Query、SAP公司的SEEED、Skyhigh Networks、CipherCloud、IntegriDB[34]以及SQL Server 2016的“始终加密”方案等项目都各有侧重地涉足这一领域。其中,SEEED面向HANA内存型数据访问系统,Big Query和Skyhigh Networks面向弱关系型,SQL Server 2016、IntegriDB的加密方案面向关系型。然而,现有的诸多解决方案有些依靠一套弱加密方案,极容易泄露敏感数据相关信息,也有些基于安全级别高的加密方案,但是无法保证复杂数据操作需求。应用程序开发商如何选择并改进一套契合的数据访问安全技术、科研人员如何弥补数据访问安全技术功能上的缺陷并提升效率、普通群众如何认知和了解不同数据访问安全技术的优劣与瓶颈,成为了这个时代的长久命题。
传统的数据访问安全往往涉及访问控制、接口控制、数据流控制和数据加密等较为广义的安全措施。目前的绝大多数数据访问安全技术为了保障基本功能,对访问控制等方面有所舍弃,即极少考虑规则制定者和规则执行者的用例。Fuller B等人[35]基于自身开发的性能评估平台,对现有诸多数据访问安全技术进行了测试。通过测试查询回复完整性、并行更新数据完整性、查询时延和吞吐量等,可看出密文查询恢复时间极度依赖于网络能力、负载、结果集大小、数据和查询子句顺序、查询子句内容、规则的存在和复杂度等方面。
CryptDB是建立于关系型数据库MySQL的数据访问安全技术,其主要组件位于三模式架构的概念模式与外模式之间,相当于应用程序与数据访问系统管理服务器之间的一个加密解密插件。作为第一个实用的、有较为完整安全性证明的数据访问安全技术,它以洋葱加密结构较好地实现了效率和安全性上的平衡。该程序通过在数据访问管理系统MySQL中拟定一些用户自定义函数,成功地实现了数据访问系统内的逐层解密,以保障对应的数据操作得以执行。其辅助插件Monomi[36]也通过添加规划器和设计师,在复杂查询的拆分规划和查询预处理等方面有显著的性能提升。
Arx[19]是建立于非关系型数据库MongoDB的数据访问安全技术,该方案借鉴了Google公司 Big Query,为了保证效率,使用时需要指定哪些是需要加密的敏感字段和这些字段将会进行的操作,这样便于程序采用对应加密算法。ArxRANGE和Arx-EQ是创新的算法。ArxRANGE用于处理范围查询和排序查询,为了便于密文比较,它采用了乱码电路的思想,利用该算法在客户端可以使用密钥k(32位系统采用1 KB)篡改程序P,并且创建一个经过模糊处理的程序ObfP。为防止服务器学习排序信息,这种算法要求主键必须加密。而Arx-EQ采用了搜索令牌树的思想,将关键字确定性加密结果和对应计数器的总体散列值作为密文,这样有效防止了攻击者通过计算某一值出现的频率而进行推理攻击。
BlindSeer[37]是Pappas等人提出的一个三方数据访问安全技术,它可缩放,旨在控制布尔查询次线性复杂度,其中三方指代两方服务器和一方用户。该方案采用一个包含叶子节点对应数据访问记录的搜索树的索引和存储后代节点关键字的布隆过滤器,再辅以YaoAC的乱码电路,成功实现了高效的布尔查询。基于现代服务器,该方案可以支持在10TB数据、1亿条数据记录和每行70项可搜索对象的数据访问系统中执行查询。
目前自治开放可使用的数据访问安全技术各有千秋,均在衡量功能性、安全性与效率之间的平衡点,使用者可根据自己的具体需求,采用或借鉴合适的数据访问安全技术。在效率方面,CryptDB相对于TPC-C的事务吞吐率下降26%左右,Arx在测试网站应用ShareLaTeX时计算耗时增加约10%,而BlindSeer对于绝大多数查询来说,性能均下降20%~300%。在功能保障方面,CryptDB支持全部关系代数和代码修改,不包括关键字查询、子串查询和通配符查询,支持多客户端、用户认证和访问控制,不支持查询协议制定;Arx支持大多数关联阵列操作,不支持布尔查询、关键字查询、子串查询和通配符查询,不支持一切行为管控、多客户端和代码改写;Blind Seer支持除了笛卡尔积的关系代数操作,支持关键字查询,不支持子串查询、通配符查询和求和操作,行为管控仅支持查询协议的制定与实施。
6 结束语
本文基于数据自治开放的大背景,分析了数据盒面临的安全挑战。通过介绍不同支持密文域处理的数据访问安全技术的原理与优劣,研讨不同攻击的条件、目标和成效,归纳现有查询转换技术和盲区,分析现有主流数据访问安全技术的应用特征与性能。支持密文域处理的数据访问安全技术目前主要针对结构良好的数据,且安全数据访问软件也以关系型数据库居多。
现有安全数据访问底层技术多在安全度和效率上做出权衡,尤其对于全同态加密、ORAM等技术仍需对效率进行大幅优化,对于保序加密、可搜索加密仍需对安全性和可验证性加以深化。数据访问安全技术也在操作上存在30%~300%的耗时增益,对体系架构的设计和优化也必将为数据自治开放模式带来新的突破。考虑到通用全同态加密的效率瓶颈以及支持密文域的数据访问安全技术难以扩展到文件、图片等类型的数据,对于大数据环境下数量庞大且格式各异的数据密文域的处理,目前的密码技术还难以提供有效的解决手段。未来需要综合密码学、数据科学技术、软件工程和系统访问控制的交叉研究,完善发展面向数据自治开放的新型数据保护机制,形成开放自治的“数据盒”。研究数据盒的新型加密机制、访问控制和监控分析机制、数据盒的遭受恶意使用或攻击时的自毁机制,是大数据环境下数据开放自治共享的重要研究方向,具有重要的理论和应用价值。
参考文献
[1]POPA R A , REDFIELD C , ZELDOVICH N ,et al. CryptDB:protecting confidentiality with encrypted query processing[C]// The 23rd ACM Symposium on Operating Systems Principles,October 23-26,2011,Cascais,Portugal. New York:ACM Press, 2011: 85-100.
[2] GENTRY C . Fully homomorphic encryption using ideal lattices[J]. ACM Symposium on Theory of Computing, 2009,9(4): 169-178.
[3] GOLDREICH O , . Towards a theory of software protection and simulation by oblivious RAMs[C]// The 19th Annual ACM Symposium on Theory of Computing,May 25-27,1987,New York,USA. New York:ACM Press, 1987: 182-194.
[4] BELLARE M , BOLDYREVA A,O’NEILL A . Deterministic and efficiently searchable encryption[C]// The 27th Annual International Cryptology Conference on Advances in Cryptology,August 19-23,2007,Santa Barbaba,USA. Heidelberg:Springer-Verlag, 2007: 535-552.
[5] BOLDYREVA A , CHENETTE N , LEE Y ,et al. Order-preserving symmetric encryption[C]// The 28th Annual International Conference on Advances in Cryptology:the Trheory and Applicaitons of Cryptographic Techniques,April 26-30,2009,Cologne,Germany. New York:ACM Press, 2009: 224-241.
[6] BOLDYREVA A , CHENETTE N,O'NEILL A . Order-preserving encryption revisited:improved security analysis and alternative solutions[C]// The 31st Annual Cryptology Conference,August 14-18,2011,Santa Barbara,USA. Heidelberg:Springer, 2011: 578-595.
[7] PANDEY O , ROUSELAKIS Y . Property preserving symmetric encryption[J]. Lecture Notes in Computer Science, 2012(7237): 375-391.
[8] AGRAWAL R , KIERNAN J , SRIKANT R ,et al. Order preserving encryption for numeric data[C]// The 2004 ACM SIGMOD International Conference on Management of Data,June 13-18,2004,Paris,France. New York:ACM Press, 2004: 563-574.
[9] KERSCHBAUM F , . Frequency-hiding order-preserving encryption[C]// The 22nd ACM SIGSAC Conference on Computer and Communications Security,October 12-16,2015,Denver,USA. New York:ACM Press, 2015: 656-667.
[10]KERSCHBAUM F , SCHRÖPFER A . Optimal average-complexity ideal-security order-preserving encryption[C]// The 2014 ACM SIGSAC Conference on Computer and Communications Security,November 3-7,2014,Scottsdale,USA. New York:ACM Press, 2014: 275-286.
[11]POPA R A , LI F H , ZELDOVICH N . An ideal-security protocol for orderpreserving encoding[C]// IEEE Symposium on Security and Privacy,May 19-22,2013,San Francisco,USA. Piscataway:IEEE Press, 2013: 463-477.
[12]DAN B , LEWI K , RAYKOVA M ,et al. Semantically secure order-revealing encryption:multi-input functional encryption without obfuscation[J]. Lecture Notesin Computer Science , 2015(9057): 563-594.
[13]CASH D , LIU F H , O'NEILL A ,et al. Reducing the leakage in practical orderrevealing encryption[J]. IACR Cryptology ePrint Archive, 2016: 661.
[14]CHENETTE N , LEWI K , WEIS S A ,et al. Practical order-revealing encryption with limited leakage[C]//International Conference on Fast Software Encryption,March 20-23,2016,Bochum,Germany. Heidelberg:Springer, 2016: 474-493.
[15]BOST R , . ∑oφoς:forward secure searchable encryption[C]// The 2016 ACM SIGSAC Conference on Computer and Communications Security,October 24-28,2016,Vienna,Austria. New York:ACM Press, 2016: 1143-1154.
[16]KAMARA S , PAPAMANTHOU C . Parallel and dynamic searchable symmetric encryption[C]// International Conference on Financial Cryptography and Data Security,April 1-5,2013,Okinawa,Japan. Heidelberg:Springer, 2013: 258-274.
[17]STEFANOV E , PAPAMANTHOU C , SHI E . Practical dynamic searchable encryption with small leakage[C]// NDSS Symposium 2014,February 23-26,2014, San Diego,USA.[S.l.:s.n.], 2014: 23-26.
[18]PODDAR R , BOELTER T , POPA R A . Arx:a strongly encrypted database system[J]. IACR Cryptology ePrint Archive, 2016: 591.
[19]YAO A C , . How to generate and exchange secrets[C]// The 27th Annual Symposium on Foundations of Computer Science,October 27-29,1986,Toronto,Canada. Piscataway:IEEE Press, 2008(10): 162-167.
[20]ROCHE D S , APON D , CHOI S G ,et al. POPE:Partial order preserving encoding[C]// The 2016 ACM SIGSAC Conference on Computer and Communications Security,October 24-28,2016,Vienna,Austria. New York:ACM Press, 2016: 1131-1142.
[21]STEFANOV E , VAN DIJK M , SHI E ,et al. Path ORAM:an extremely simple oblivious RAM protocol[C]// The 2013 ACM SIGSAC Conference on Computer & Communications Security,November 4-8,2013,Berlin,Germany. New York:ACM Press, 2013: 299-310.
[22]GARG S , MOHASSEL P , PAPAMANTHOU C . TWORAM:roundoptimal oblivious ram with applications to searchable encryption[J]. Journal of Chinese Agricultural Mechanization, 2015: 1010.
[23]RIVEST R , SHAMIR A , ADLEMAN L M . A method for obtaining digital signatures and public-key cryptosystems[J]. Communications of the ACM, 1983,26(2): 96-99.
[24]ELGAMAL T . A public key cryptosystem and a signature scheme based on discrete logarithms[J]. IEEE Transactions on Information Theory, 1985,31(4): 469-472.
[25]PAILLIER P , . Public-key cryptosystems based on composite degree residuosity classes[C]// International Conference on Theory and Application of Cryptographic Techniques,May 2-6,1999,Prague,Czech Republic. Heidelberg:Springer, 1999: 223-238.
[26]GOLDWASSER S , MICALI S . Probabilistic encryption[J]. Journal of Computer &System Sciences, 1984,28(2): 270-299.
[27]DAN B , GOH E J , NISSIM K . Evaluating 2-DNF Formulas on Ciphertexts[C]// The 2nd International Conference on Theory of Cryptography,February 10-12,2005,Cambridge,USA. Heidelberg:Springer, 2005(3378): 325-341.
[28]VAN D M , GENTRY C , HALEVI S ,et al. Fully homomorphic encryption over the integers[C]// Annual International Conference on the Theory and Applications of Cryptographic Techniques,April 30-May 4,Paris,France. Heidelberg:Springer, 2010: 24-43.
[29]CORON J S , MANDAL A , NACCACHE D ,et al. Fully Homomorphic Encryption over the Integers with Shorter Public Keys[C]// The 31st Annual Conference on Advances in Cyptology,August 14-18,2011,Santa Barbara,USA. Heidelberg:Springer, 2011: 487-504.
[30]CORON J S , LEPOINT T , TIBOUCHI M . Scale-invariant fully homomorphicencryption over the integers[M]// The 17th IACR International Conference on Practice and Theory of Public-Key Cryptography,March 26-28,2014,Buenos Aires,Argentina. Heidelberg: Springer, 2014: 361-372.
[31]BRAKERSKI Z , GENTRY C , VAIKUNTANATHAN V . (Leveled) fully homomorphic encryption without bootstrapping[J]. ACM Transactions on Computation Theory (TOCT), 2014,6(3): 13.
[32]BRAKERSKI Z , VAIKUNTANATHAN V . Efficient fully homomorphic encryption from (standard) LWE[C]//Foundations of Computer Science,October 23-25,2011,Palm Springs,USA. Piscataway:IEEE Press, 2011: 97-106.
[33]GENTRY C , HALEVI S , SMART N P . Fully homomorphic encryption with polylog overhead[C]//Advances in Cryptology EUROCRYPT 2012,April 15-19,2012,Cambridge,UK. Heidelberg:Springer, 2012: 1-16.
[34]ZHANG Y , KATZ J , PAPAMANTHOU C . IntegriDB:Verifiable SQL for outsourced databases[C]//The 22nd ACM SIGSAC Conference on Computer and Communications Security,October 12-16,2015,Denver,USA. New York:ACM Press, 2015: 1480-1491.
[35]FULLER B , VARIA M , YERUKHIMOVICH A ,et al. SoK:Cryptographically Protected Database Search[C]//The 38th IEEE Symposium on Security and Privacy,May 22-24,2017,San Jose,USA. Piscataway:IEEE Press, 2017: 172-191.
[36]TU S , KAASHOEK M F , MADDEN S ,et al. Processing analytical queries over encrypted data[C]//International Conference on Very Large Data Bases,August 26-30,2013,Riva del Garda,Italy. New York:ACM Press, 2013: 289-300.
[37]FISCH B A , VO B , KRELL F ,et al. Malicious-client security in blind seer:a scalable private DBMS[C]//IEEE Symposium on Security and Privacy,May 18-20,2015,San Jose,USA. Piscataway:IEEE Press, 2015: 395-410.