
熊 赟1,2,朱扬勇1,2
1.复旦大学计算机科学技术学院 上海 201203;
2.上海市数据科学重点实验室(复旦大学) 上海 201203
(引用标注:熊赟,朱扬勇.特异群组挖掘:框架与应用[J].大数据,2015(2):66-77.)
摘要 特异群组挖掘在证券金融、医疗保险、智能交通、社会网络和生命科学研究等领域具有重要应用价值。特异群组挖掘与聚类、异常挖掘都属于根据数据对象的相似性来划分数据集的数据挖掘任务,但是,特异群组挖掘在问题定义、算法设计和应用效果方面不同于聚类和异常等挖掘任务。为此,系统地阐述了特异群组挖掘任务,分析了特异群组挖掘任务与聚类、异常等任务之间的差异,给出了特异群组挖掘任务的形式化描述及其基础算法,最后,列举了特异群组挖掘的几个重点应用。
关键词 大数据;数据挖掘;特异群组;聚类;异常检测;数据相似性
Abstract Abnormal groups can be found in a wide range of areas. Together with clustering and outlier detection, their goals are all to partition a data set according to data similarity. However, abnormal group mining (AGM) is different in problem definition, algorithm design and applications. To the best of our knowledge, the abnormal group mining problem was investigated systematically. The differences among AGM, clustering and outlier detection were analyzed. The formalized definitions on AGM and a framework algorithm were presented, and several interesting applications were particularized.
Key words big data, data mining, abnormal group, clustering, outlier detection, data similarity
1 引言
数据挖掘技术是数据开发技术的核心[1]。其中,挖掘高价值、低密度的数据对象是大数据的一项重要工作,甚至高价值、低密度常常被用于描述大数据的特征[2]。存在这样一类数据挖掘需求:将大数据集中的少部分具有相似性的对象划分到若干个组中,而大部分数据对象不在任何组中,也不和其他对象相似(如图1所示)。将这样的群组称为特异群组,实现这一挖掘需求的数据挖掘任务被称为特异群组挖掘,由朱扬勇和熊赟于2009年首次提出[3]。参考文献[3]中,特异群组的英文用peculiarity group表示,意指这些群组具有特殊性、异常性;参考文献[4]强调这些群组中的对象具有强相似性、紧粘合性(即cohesive),因此将特异群组挖掘问题的英文进一步深化,表达为cohesive anomaly mining,意指挖掘的特异群组不仅具有特殊性、异常性,而且群组对象是强相似、紧粘合的。将这些对象形成的群组改用abnormal group[4]表示。
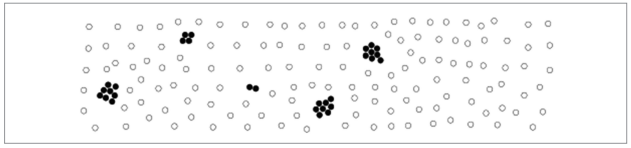
图1 大数据集里的特异群组
大数据特异群组挖掘具有广泛应用背景,在证券交易、智能交通、社会保险、生物医疗、银行金融和网络社区等领域都有应用需求,对发挥大数据在诸多领域的应用价值具有重要意义。例如,在证券市场中,特异群组常常表现为合谋操纵(多账户联合操纵)、基金“老鼠仓”等。这些账户以获取不正当利益为目的,集中资金优势或利用信息优势,操纵交易量、交易价格,扰乱市场秩序。其中,合谋操纵的行为模式主要是集中资金优势、持股优势进行市场操纵,通过使用多个账户进行分工交易、分仓持有来合谋操纵市场价格和成交量,以诱导其他投资者;基金“老鼠仓”的行为模式是通过获悉基金即将或正在交易某投资标的,且该笔交易大幅影响投资标的价格的交易信息,以相近时刻、相同买卖方向用个人私有资产同步交易该投资标的,以获取收益。本文系统地阐述了特异群组挖掘任务的框架,分析了特异群组挖掘任务与聚类、异常等任务之间的差异,给出了特异群组挖掘任务的形式化描述及其基础算法,最后,列举了特异群组挖掘的几个重点应用。
2 特异群组挖掘与聚类和异常检测的关系
特异群组是指由给定大数据集里面少数相似的数据对象组成的、表现出相异于大多数数据对象而形成异常的群组[3,4],是一种高价值低密度的数据形态。特异群组挖掘、聚类和异常检测都是根据数据对象间的相似程度来划分数据对象的数据挖掘任务,但它们在问题定义、算法设计和应用效果上存在差异[5]。
2.1 与聚类的比较
聚类是根据最大化簇内相似性、最小化簇间相似性的原则,将数据对象集合划分成若干个簇的过程[6]。相似性是定义一个簇的基础,聚类过程的质量取决于
相似性函数的设计,不同的簇相似性定义将得到不同类别的簇[7]。例如,参考文献[7]给出了几种不同类别的簇:图2(a)表示明显分离的簇,每个对象到同一簇中对象的距离比到不同簇中任意对象的距离更近或更相似;图2(b)表示基于原型的簇,每个对象到定义该簇的原型的距离比到其他簇的原型的距离更近或更相似;图2(c)是基于密度的簇,簇是对象的稠密区域;图2(d)表示一种概念簇,簇是有某种共同性质的对象的集合。可以看出,具有某种共同性质的对象取决于挖掘目标的定义。不同的簇相似性定义得到不同的簇,甚至还有不同形状、不同密度的簇。
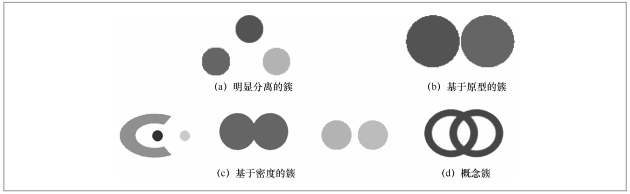
图2 不同相似性定义下的各种簇[7]
但不管怎样,传统聚类算法是处理大部分数据对象具有成簇趋势的数据集,将大部分数据对象划分成若干个簇。然而,在一些大数据应用中,大部分数据并不呈现聚类趋势,而仅有少部分数据对象能够形成群组。
特异群组挖掘是在大数据集中发现特异群组,找出的是少部分具有相似性的数据对象。与聚类的共同之处是,特异群组中的对象也具有相似性,并将相似对象划分到若干个组中,这在一定程度上符合传统簇的概念。但是,特异群组之外的对象数目一般远大于特异群组中对象的数目,并且这些对象不属于任何簇,这和聚类的目的是不同的。
2.2 与异常检测的比较
少部分数据对象的挖掘通常被认为是异常检测任务[8]。在特异群组挖掘问题中,相对于不在任何群组中的大部分数据对象而言,少部分相似对象形成的群组是一种异常。但是,现有的异常检测算法难以直接用于特异群组挖掘。一是,目前大多数异常挖掘算法的目标是发现数据集中那些少数不属于任何簇,也不和其他对象相似的异常点(point anomalies)[9],这和特异群组的目标不同;二是,除异常点检测外,存在一些算法用于发现异常点成簇的情况,称为微簇(micro-cluster或clustered anomalies)挖掘[10,11],但是该任务也对剩下的大部分数据有聚类假设,即微簇问题在一个数据集中包含点异常、微簇和簇,这不同于特异群组挖掘;三是,集体异常(collective anomalies)挖掘任务也不同于特异群组挖掘,因为集体异常只能出现在数据对象具有相关性的数据集中,其挖掘要求探索数据集中的结构关系[9]。目前集体异常挖掘主要处理序列数据、图数据和空间数据。
2.3 三者关系
通过上述比较分析可以得到,如果一个数据集中的大部分数据对象都能够归属于某些簇,那么那些不能归属于任何簇的数据对象就是异常对象;如果一个数据集中的大部分数据对象都不属于任何簇,那么那些具有相似性的数据对象所形成的群组就是特异群组。因此,挖掘的需求决定了簇、特异群组、异常点:如果需要找大部分数据对象相似,则是聚类问题;需要找少部分数据对象相似,则为特异群组;如果是找少数
相似的数据对象,则为异常。
综上,特异群组挖掘结合了聚类和异常检测的一些特点,但又具有自身的特性。特异群组挖掘所关注的是一个大数据集中大部分数据对象不相似,而每个特异群组中的对象是相似的。即特异群组对象的群体性和普通对象的个体性不同,群组中的个体对象本身单独而言并不一定特异,只是和群组中的相关对象一起构成了特异群组。
3 特异群组挖掘形式化描述[4]
设Fd为d-维特征空间,D={O1, O2 ,…, Oi ,…,On }是对象集合,Oi ∈Fd。两个对象Oi和Oj间的相似性f由相似性函数sim(Oi,Oj )计算(0≤f≤1)。
定义1(相似对象)给定一个相似性阈值δ,对于一个对象Oi(Oi ∈D),如果数据集中至少存在另一个对象Oj,使得sim(Oi, Oj )≥δ。那么对象Oi称为对象集合D中关于δ的相似对象。
在特异群组挖掘问题中,由于大部分数据对象都是
相似的,只有群组中的对象才是相似对象,表现出相异于大部分对象的特性,因此,在特异群组挖掘问题中,相似对象被称为特异对象,特异对象的集合记为P,剩下不在P中的对象记为D\P。相应地,度量数据对象是否为相似对象的相似性函数被称为特异度度量。特异度度量是定义一个特异群组的基础。
对于一个数据集,形成特异群组集合的数据对象相对整个数据集中的数据对象是少数的。在很多情况下,指定合适的相似性阈值对用户而言是困难的。例如,在证券市场合谋操纵账户挖掘中,多个账户在一定时间段内的多次相同交易行为是价格操纵的基本行为。简单直观地,可以以相同交易行为的数量l来定义两个账户的相似度,用这个数量作为相似性阈值。然而,在实际实施过程中,这个相似性阈值对用户而言是困难的。
但是,对于特异群组挖掘需求而言,用户更容易知道的是他们希望发现的特异对象的数量。例如,作为证券监管者,希望发现的是涉嫌操纵股价的账户数量。进一步,特异群组挖掘问题是挖掘“少量”数据对象构成的特异群组,一般观点认为20%已经很少了,但在许多应用中,如证券市场合谋操纵账户挖掘这个例子中,10%都不是“少量”,操纵账户可能小于0.2%或更小,才被认为是“少量”,这个数量完全由实际问题的用户理解所决定。例如,用户可以根据预算的经费和时间等指定其期望的特异对象数量。同时,这也是用户的直接需求,用户易于理解和指定。于是,对特异群组挖掘问题进行定义。
定义2(τ-特异群组挖掘)特异群组挖掘是在一个数据集中发现特异群组的过程,这些特异群组形成的集合包含τ个数据对象,τ是一个相对小的值(τ<<n×50%n是数据集中对象总个数)。
性质1(相似性阈值的存在性)给定一个特异对象的数量的阈值τ,存在一个潜在的相似性阈值δ,对于τ个特异对象形成的集合P中每一个对象O,都存在至少另一个对象Q与其相似,sim(O,Q)≥δ。性质1说明了数据集中具有相似性的数据对象(特异对象)的数量τ可以反映数据集中对象间的相似性阈值,即选择一个特异对象数量作为代替相似性阈值的方法是合适的。
特异对象的数量τ不仅易于用户描述其需求,而且因为τ相对较小,算法可以利用τ设计剪枝策略,以提高大数据集特异群组挖掘算法的效率。
定义3(对象的特异度评分,特异对象)一个对象Oi的特异度评分ω是Oi和该数据集中其他对象间的最大相似性值,即ω(Oi)=maxl≤j≤n, j≠i S(Oi ,Oj ),其中S(Oi ,Oj )表示对象Oi和Oj的相似性度量值。给定一个特异度评分阈值δ>0,当一个对象O的特异度评分ω(Oi )>δ,则该对象O是一个特异对象。表示在整个数据集中特异对象的集合。在特异度评分定义的基础上,定义特异群组。
定义4(特异群组)一个特异对象的集合G是一个候选特异群组,当且仅当|G|≥2,并且G中的每两个对象都是相似的,即对于Oi,Oj∈G,有S(Oi ,Oj )|≥δ。如果不存在任何一个G的超集是一个候选特异群组,那么G是一个特异群组。特异群组的紧致性度量如下。
定义5(紧致性)一个特异群组G的紧致性ζ是该群组中所有对象的总体特异度评分之和,即ζ=∑i=1|G|ω(Oi)(Oi∈G)。
设是特异群组集,的紧致度是中所有特异群组紧致度之和。前已述及,特异度评分阈值δ在实际应用中用户是很难设置的。为了克服这个困难,用户可以设置一个特异群组集合的对象总数阈值τ,这对于用户以及特异群组挖掘问题本身而言是一个容易设置和接受的阈值。这两个阈值(τ和δ)之间的关系如下。
给定一个相对小的阈值τ(τ≥2)(特异群组集合中的对象个数相对较少,因此τ的值相对较小),可以找到具有最高特异度评分的τ个对象。那么,第τ个对象的特异度评分就是相应的特异度评分阈值δ,即这τ个对象具有最高的特异度评分值,并且包含τ个对象的特异群组集的紧致度最大。
在对象特异度评分定义基础上,给出进一步深化的特异群组挖掘任务定义。
定义6(τ-特异群组挖掘)特异群组挖掘问题是找到数据集中所有的特异群组,满足特异群组集合的紧致度最大,且||=τ,其中τ(τ≥2)是一个给定阈值。
4 特异群组挖掘框架算法[4]
对于τ-特异群组挖掘问题,传统的聚类算法无法直接使用。因为,聚类算法通常要求用户指定一个相似性阈值(或相关参数),而这样的限制不能保证结果中相似对象的数量满足阈值τ。一种修改是通过多次调用聚类算法调整参数值,终止的条件是当簇中对象的数量满足用户指定的数量τ。但是,由于重复多次的聚类算法调用,造成大量冗余的计算。更坏的情况是,当多个参数之间相关时,这是相当困难的。
虽然,层次聚类方法看上去能够简单地使用一个对象数量的阈值作为参数提前终止聚类,且易于处理任何形式的相似性。然而,对象间相似性的计算具有相当高的复杂度[12]。
还有一些聚类算法给出如何选择参数阈值的指导(如DBSCAN算法中的MinPts=4[13])或者自动调整参数阈值(如SynC算法[14])。但是,对于一般用户,根据参数阈值指导选择参数仍然是一项困难的工作,并且算法推荐的默认值在很多情况下并不适合,因此用户仍然必须做出许多尝试;而自动参数调整方法在某些应用场景中会显示出局限性,例如当为了满足特异群组中用户指定数量τ对象时,自动策略如SynC中的MDL(minimum description length)原则并不适合。此外,Top-c聚类[15]是一种试图将相似性度量阈值转化为簇个数的聚类算法,即将数据集中的数据对象划分到符合
质量定义的c个簇中,然而,簇的数量c并不能决定对象的数量,即c个簇可能包含数据集中大量的数据对象(如70%)。
因此,简单地修改聚类算法处理τ-特异群组挖掘问题不是很好的解决方案,原因是两者的目的不同。
值得指出的是,Gupta等提出bregman bubble clustering(BBC)算法[16]挖掘c个密集的簇,包含τ个对象,这和特异群组挖掘问题的出发点相似。然而,一方面,BBC算法需要指定c个簇的代表点,然后将对象指定到与代表点相近的对象中,直到τ个点被聚类。对于用户而言指定这样的代表点是困难的;另一方面,BBC试图同时限制对象的数量和簇的数量c,因此又遇到了τ个对象必须划分到c个簇的困境。
考虑到上述问题,下面给出一个特异群组挖掘(abnormal group mining, AGM)框架算法。该算法是一个两阶段算法[4],如图3所示。第一阶段是找到给定数据集中的最相似的数据对象对,并采用剪枝策略将不可能包含特异对象的对象对删除,然后从候选对象对中计算得到特异对象;第二阶段将对象对划分到特异群组中。

图3 τ-特异群组挖掘算法框架[4]
在第一阶段,采用Topk相似点对查询策略找到Top k个相似点对,在这些相似点对中的对象被认为是候选对象。不难证明,k与τ之间的关系为k=τ×(τ-1)/2。因为τ是一个相对小的数,对于较小的k,具有剪枝策略的Top k相似点对查询算法[17~19]有良好的运行效率。即使对于高维数据对象,相似点对查询算法复杂度也可以降到O((dn/B)1.5)[18],其中d为数据对象的维度,n为数据对象集中对象数,B为数据集所在外存页字节数。之后,在获得的Topk个点对中找到Topτ个具有最大特异度评分的对象作为特异对象。
在第二阶段,根据特异群组定义,特异群组中的每对对象之间必须相似,因此特异群组事实上是一个最大团,采用最大团挖掘算法[20,21]将所有的τ个特异对象划分到相应的特异群组中。最大团挖掘的最坏情况时间复杂度为O(3τ/3)[21](τ为图的顶点数),因为特异群组挖掘算法第一阶段的输出为Topτ个对象,而τ是一个相对较小的数,因此,对τ个数据对象集发现其最大团而言,特异群组挖掘算法具有较好效率。
5 特异群组挖掘应用
行为数据反映了人类的各种行为方式,这些行为通常是个体对象主动的行为(如股票交易、看病就医、通勤出行、购物等),一般情况下,行为对象具有个体性。因此,如果有两个或两个以上的对象长时间存在共同的行为,说明这些对象具有群体组织性,有别于通常大部分对象的个体性,这些群体是异常现象。特异群组挖掘就是在众多行为对象中找到那些少数对象群体,这些行为对象具有一定数量的相同或相似行为模式,表现出相异于大多数对象而形成异常的群组,目前已有相当的应用。
(1)证券市场操纵行为
挖掘老鼠仓“马乐案”中,原博时基金经理马乐利用任职优势,与他人共同操作其亲友等开立的一批账户(关系账户自然人赵秋怡、疑似隐匿于银河证券客户信用交易担保证券账户等),先于或同步于其管理的博时基金多次买入、卖出相同个股(与博时精选基金相关的“众生药业”、“迪威视讯”等多支股票),如图4所示。这些账户隐蔽性强,在过程中没有散发传播虚假消息,也没有可供披露的提升上市公司价值的经营活动等,难以甄别,查处成本高。然而,这批账户通常在多天具有共同的股票交易行为,且异于其他大多数账户,是一种异常现象,形成特异群组。因此,特异群组挖掘技术将有助于发现这些可疑账户。
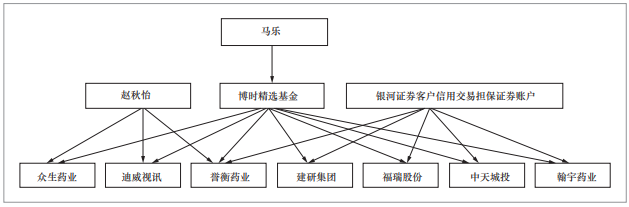
图4 “老鼠仓”可疑账户及操纵的股票[22]
(2)医疗保险中的保费欺诈行为挖掘[3]
我国基本医疗保险中,参保人使用医保卡就医发生费用时,由医保基金支付医保范围内的费用,超出医保范围的费用才需要个人现金支付。为保证医保基金的正常安全运转,医保机构对参保人医保消费行为有一定的限制,如参保人只能消费与病情和处方相关的药品,而不允许超范围配药,个人医保费用只允许用于本人就诊、购药等。由于每张医保卡的使用限制,一种典型的用卡欺诈行为是“医保卡套现”,即嫌疑者使用多张医保卡获得尽可能多的药品,然后卖出获取利益。正常情况下,个人使用医保卡就医是个体行为,因此嫌疑者使用一批医保卡(即多个医保卡账户)多天在多个或同一个医院进行刷卡购买药品的行为是一种异常现象。医保监督局希望能够找到这样的欺诈行为账户予以监管。图5是特异群组挖掘算法在上海市医保基金风险防控中的应用展示。图5(a)展示了7个特异群组,并给出了每个特异群组在多少天(“群组长度”)有一致的行为,“包含卡数”表示该群组中的特异对象;图5(a)的右下方还给出了有特异群组出现的一些医院示例。图5(b)将第一群组中的5个特异对象展开(考虑到隐私,已隐去身份证号,并且医保卡号和姓名也做了一定的脱敏处理)。图5(b)也展示了这些特异群组所持医保卡一般套现的药品名称和费用。
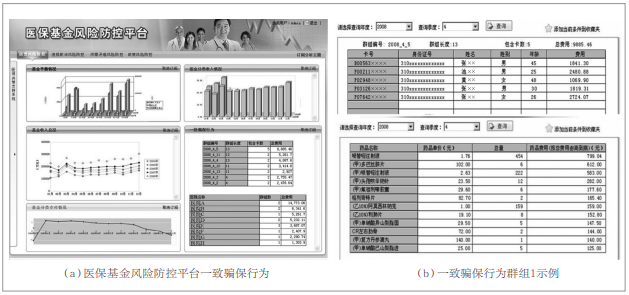
图5 医疗保险中的保费欺诈行为挖掘
右下方还给出了有特异群组出现的一些医院示例。图5(b)将第一群组中的5个特异对象展开(考虑到隐私,已隐去身份证号,并且医保卡号和姓名也做了一定的脱敏处理)。图5(b)也展示了这些特异群组所持医保卡一般套现的药品名称和费用。
(3)智能交通监控应用中的驾车犯罪团伙挖掘
以汽车为作案工具的犯罪案件中,一种常见的情况是多辆汽车共同参与作案。作案车辆为熟悉作案地点和行程,通常会提前准备,在多天内共同出现在多个地点,随着智能交通技术的发展,这些信息都将由高清摄像头识别记录。由于城市道路上的车辆行驶以个体行为为主,因此这种有一批车辆在多天共同出现在多个监控点的行为是一种异常现象。警察机关希望能够从监控数据库中挖掘到这些车辆,为案件侦破提供线索[3]。图6是特异群组挖掘算法在上海市宝山公安分局关于跟车行为检测中的应用展示,通过挖掘可以得到在多天共同出现在多个监控点的异常车辆群组(考虑到隐私,图6中的车牌数据也进行了一定的脱敏处理)。
图6 公安系统跟车行为检测
(4)电子商务交易中的信誉欺诈挖掘
大多数在线交易平台(如eBay.com和Taobao.com)都已建立交易双方的信用评分系统。对卖家而言,更高的信用等级将带来更多买家,然而,从低等级到高等级需要经过较长时间积累大量的交易。于是,一些卖家采用“刷信用”方式赚取高等级的信用评分。提供“刷信用”服务的嫌疑者(甚至是专门的“刷信用”公司)通常申请一批账号与所服务卖家事先商定,在不进行实际交易的方式下给出好的信用评分。同时,这批账号又为其他多个卖家“刷信用”。相比所有在线客户,“刷信用”账号数量是相对较少的。因此,如果一组账户总是给大量相同的卖家好的信用评分,那么这组账户是可疑的。发现这些可疑账户将为交易平台信誉欺诈检测提供帮助。
(5)社会网络中的小群体发现
Leskovec等人发现社会网络中,社区变得越大,社区成员的交流却开始变得更少[23]。因此,在这样庞大的社会网络中识别交流更加密集的小社区变得更有意义,虽然他们仅仅包含非常少的节点,即真正具有成为社区趋势的对象数量相对整个社会网络的节点而言是少部分。在大规模的社会网络中挖掘小社区群体属于特异群组挖掘问题。
(6)论文抄袭检测
大多数论文都是不相同的,但是仍然存在一些抄袭的论文。例如,几篇论文抄袭同一篇,或者A抄袭B,B抄袭C,甚至出现专门的论文代写公司,这些抄袭的论文事实上构成一系列的特异群组。然而,现有的Similarity Join方法[24]目的只是发现抄袭论文的对象对,而不能发现多篇抄袭论文形成的特异群组。除了在社会行为科学研究中特异群组挖掘具有广泛的应用背景,科学研究领域(如生命科学研究)产生的科学数据也有着重要的价值。
(7)在生命科学研究中的特异群组挖掘
生物学家总是希望对实验收集的基因或蛋白质序列进一步分析,如识别蛋白质序列所属的家族。聚类是常用的方法,然而这些方法总是有大量的假阳性。这是因为,在一些实验收集的序列数据集中,仅仅少部分序列可能是相似的。尽管如此,传统的聚类方法将大部分序列划分到簇中。例如,Zheng等人指出许多人类转录因子(transcription factor,TF)仅仅能调控几个甚至一个下游基因[24](如TF adenosine deaminase domain-containing protein2(ADAD2)仅仅调控下游基因MUC5AC,而actin filament-associated protein 1-like 1(AFAP1L1)仅仅调控基因CAV1)。因此,如果一个生物学家收集一个基因表达数据集,大多数下游基因被不同的TF调节,而仅仅少部分由相同的TF调节。当研究调控机制时,发现少部分被相同TF调控的基因形成的簇更为合理,而不是聚类所有的数据对象。参考文献[4]对特异群组挖掘算法进行了性能评估实验,对比的算法主要是经典的聚类算法DBSCAN、BBC、SynC以及基于无剪枝的数据对象两两比对的NavAllPairs算法,如图7所示。重叠分数(overlapping score,OS)是被预测出的群组中的数据对象与已知类中的数据对象匹配的数量比例。ARI(adjusted rand index)是Hubert等提出的一种常用的有效性度量指标[26],评估预测群组与已知类的一致程度。实验结果表明,从效率上看,特异群组挖掘算法的运行时间随着数据对象数量的增长变化不大,具有较高的可伸缩性,而其他算法的运行时间增长较快;在有效性方面,在相似对象密集的情况(即τ的值越小的情况)下,有效性越高,这进一步说明,特异群组挖掘算法对于高价值、低密度的数据集具有更好的性能。
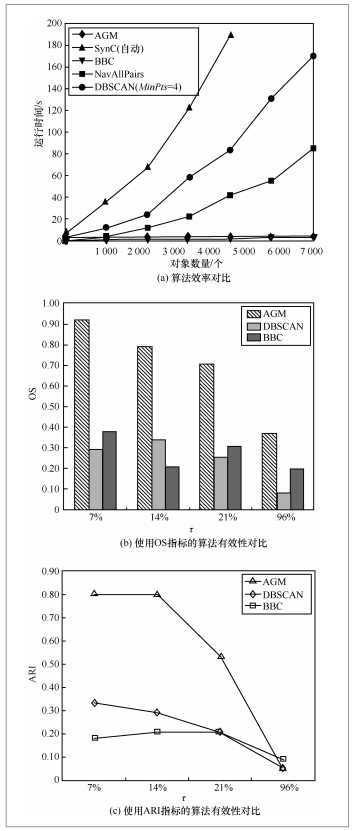
图7 在生物数据集上特异群组挖掘算法性能[4]
此外,在公共安全方面发现突发群体事件,在社交网络大数据中发现影响安全、和谐网络环境的特异群体等都是大数据特异群组挖掘的应用需求。通过对特异群组挖掘与利用,减少欺诈行为,提高监管力度,提升公共安全管理和应急响应能力,帮助政府节省开支。
6 结束语
特异群组挖掘是大数据的一个重要任务。本文讨论了特异群组挖掘任务在问题定义、算法实现和应用等方面与聚类、异常检测之间的差异,指出挖掘的需求决定了簇、特异群组、异常点的本质,表明了相似性理论是大数据挖掘技术研究的基础和关键;给出了一个易于理解和应用的特异群组挖掘任务的形式化描述及其实现算法;描述了特异群组挖掘的一些应用领域,实现大数据价值。
值得指出的是,聚类、特异群组挖掘、异常检测都是基于数据对象的相似性来挖掘数据对象的。对于给定的数据集和相似性定义。如果相似点的数量远大于孤立点的数量,对应的相似点集是聚类的结果簇,而孤立点是异常检测需要找出的数据对象;如果相似点的数量远小于孤立点的数量,相似点构成的组就是特异群组。相似点集挖掘是未来的一个重要研究方向。
参考文献
[1]朱扬勇,熊赟.大数据是数据、技术,还是应用.大数据,2015007 Zhu Y Y, Xiong Y. Defining big data. Big Data Research, 2015007
[2] Mark B. Gartner says solving ‘big data’ challenge involves more than just managing volumes of data. http://www.gartner.com/newsroom/ id/1731916, 2011
[3] Xiong Y, Zhu Y Y. Mining peculiarity groups in day-by-day behavioral datasets. Proceedings of IEEE International Conference on Data Mining (ICDM’09), Miami, Florida, USA, 2009: 578~587
[4] Xiong Y, Zhu Y Y, Yu Philip S, et al. Towards cohesive anomaly mining. Proceedings of the 27th AAAI Conference on Artificial Intelligence (AAAI-13), Bellevue, Washington, USA, 2013
[5]朱扬勇,熊赟.数据挖掘新任务:特异群组挖掘.中国科技论文在线.
[6] Jain A K. Data clustering: 50 years beyond k-means. Pattern Recognition Letters, 2010, 31(8): 651~666
[7] Tan P N, Steinbach M, Kumar V. Introduction to Data Mining. Boston: Addison-Wesley, 2006
[8] Hawkins D. Identification of Outliers. London: Chapman and Hall, 1980: 2~26
[9] Chandola V, Banerjee A, Kumar V. Anomaly detection: a survey. ACM Computing Surveys, 2009, 41(3): 1~58
[10] Papadimitriou S, Kitagawa H, Gibbons P B. Loci: fast outlier detection using the local correlation integral. Proceedings of the 19th International Conference on Data Engineering, Bangalore, India, 2003, 315~327
[11] Liu F T, Ting K M, Zhou Z H. On detecting clustered anomalies using SCiForest. Proceedings of ECML/PKDD, Barcelona, Spain, 2010: 274~290
[12] Dettling M, Buhlmann P. Supervised clustering of genes. Genome Biology, 2002, 3(12): 129~137
[13] Ester M, Kriegel H P, Sander J. A density-based algorithm for discovering clusters in large spatial databases with noise. Proceedings of the 4th International Conference on Knowledge Discovery and Data Mining, Portland, USA, 1996: 226~231
[14] Bohm C, Plant C, Shao J. Clustering by synchronization. Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, USA, 2010: 583~592
[15] Jiang D X, Pei J, Zhang A D. A general approach to mining quality pattern-based clusters from microarray data. Proceedings of DASFAA, Beijing, China, 2005: 188~200
[16] Gupta G, Ghosh J. Bregman bubble clustering: a robust, scalable framework for locating multiple, dense regions in data. Proceedings of the 6th International Conference on Data Mining, Hong Kong, China, 2008: 232~243
[17] Corral A, Manolopoulos Y, Theodoridis Y. Algorithms for processing k-closest-pair queries in spatial databases. Data & Knowledge Engineering Journal, 2004(49): 67~104
[18] Tao Y F, Yi K, Sheng C, et al. Efficient and accurate nearest neighbor and closest pair search in high-dimensional spase. ACM Transactions on Database Systems, 2010, 35(3):1~46 [19] Xiong Y, Zhu Y Y, Yu Philip S. Top-k similarity join in heterogeneous information networks. IEEE Transactions on Knowledge & Data Engineering, 2015, 27(6): 1710~1723
[20] Cheng J, Ke Y P, Fu A W. Finding maximal cliques in massive networks. ACM Transactions on Database Systems, 2011, 36(4): 1~34
[21] Tomita E, Tanaka A, Takahashi H. The worstcase time complexity for generating all maximal cliques and computational experiments. Theoretical Computer Science, 2006, 363(1):28~42
[22]赵迪.原博时基金经理马乐“老鼠仓”深度调查.股市动态分析,2013 Zhao D. The in-depth investigation of Ma Le “rat trading” at bosera select equity investment fund. Journal of Dynamic Analysis in Stock Market, 2013
[23] Leskovec J, Lang K J, Mahoney M W. Empirical comparison of algorithms for network community detection. Proceedings of the 19th International World Wide Web Conference, Raleigh, North Carolina, USA, 2010: 631~640
[24] Feng J, Wang J, Li G. Trie-join: a trie-based method for efficient string similarity joins. The VLDB Journal, 2012, 21(4): 437~461
[25] Zheng G Y, Tu K, Yang Q. ITFP: an integrated platform of mammalian transcription factors. Bioinformatics, 2008, 24(20): 2416~2417
[26] Hubert L, Arabie P. Comparing partitions. Journal of Classification, 1985, 2(1):193~218